Skillnad mellan versioner av "Superpositionsprincipen"
Pagge (diskussion | bidrag) |
Pagge (diskussion | bidrag) |
||
| Rad 1: | Rad 1: | ||
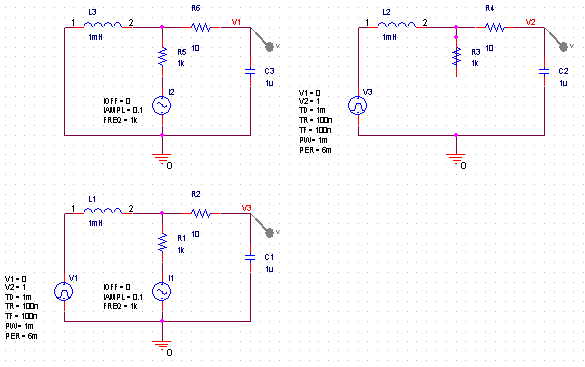
Superpositionsprincipen är ett användbart verktyd vid analys av kretsar bestående av [[Linjära komponenter]]. Den lyder "Om man vill ha utsignalen som orsakas av flera obereoende källor så kan man räkna på källorna en och en och addera resultaten istället för att räkna med alla på en gång". När man räknar på en källa sätter man alla andra till 0. En nollad strömkälla är ett avbrott (Ingen ström kan ju passera ett avbrott oavsett spänning) och en nollad spänningskälla är en kortslutnin (Ingen spänning ligger över en kortslutning oavsett ström). | Superpositionsprincipen är ett användbart verktyd vid analys av kretsar bestående av [[Linjära komponenter]]. Den lyder "Om man vill ha utsignalen som orsakas av flera obereoende källor så kan man räkna på källorna en och en och addera resultaten istället för att räkna med alla på en gång". När man räknar på en källa sätter man alla andra till 0. En nollad strömkälla är ett avbrott (Ingen ström kan ju passera ett avbrott oavsett spänning) och en nollad spänningskälla är en kortslutnin (Ingen spänning ligger över en kortslutning oavsett ström). Nedan ett exempel med två oberoende källor. | ||
[[Bild:Superposition-scematic.jpg]] | [[Bild:Superposition-scematic.jpg]] | ||
| Rad 6: | Rad 6: | ||
[[Bild:Superposition-result.jpg]] | [[Bild:Superposition-result.jpg]] | ||
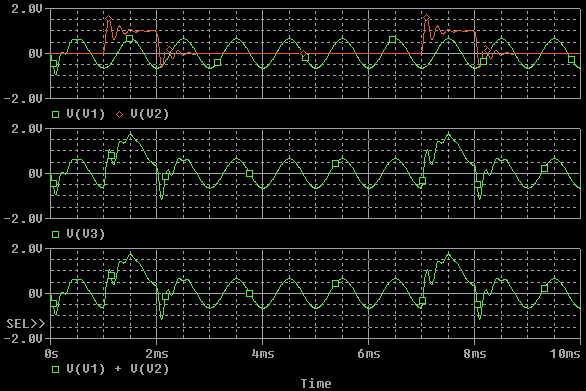
V1 är spänningen orsakad av den oberoende strömkällan, V2 spänningen orsakad av den oberoende spänningskällan, V3 spänningen då båda är påslagna samtidigt. Notera hur nollade strömkällor/spänningskällor modeleras med avbrott/kortslutning respektive. Som superpositionsprincipen förutsa så är V3 = V2 + V1. Viktigt att komma ihåg är som sagt att resultatet bara gäller för kretsar bestående av [[Linjära komponenter]]. Den stora vinsten med superpositionsprincipen inser man | V1 är spänningen orsakad av den oberoende strömkällan, V2 spänningen orsakad av den oberoende spänningskällan, V3 spänningen då båda är påslagna samtidigt. Notera hur nollade strömkällor/spänningskällor modeleras med avbrott/kortslutning respektive. Som superpositionsprincipen förutsa så är V3 = V2 + V1. Viktigt att komma ihåg är som sagt att resultatet bara gäller för kretsar bestående av [[Linjära komponenter]]. Den stora vinsten med superpositionsprincipen inser man kanske först man arbetar med [[Småsignalscheman]]. | ||
Versionen från 4 oktober 2006 kl. 11.53
Superpositionsprincipen är ett användbart verktyd vid analys av kretsar bestående av Linjära komponenter. Den lyder "Om man vill ha utsignalen som orsakas av flera obereoende källor så kan man räkna på källorna en och en och addera resultaten istället för att räkna med alla på en gång". När man räknar på en källa sätter man alla andra till 0. En nollad strömkälla är ett avbrott (Ingen ström kan ju passera ett avbrott oavsett spänning) och en nollad spänningskälla är en kortslutnin (Ingen spänning ligger över en kortslutning oavsett ström). Nedan ett exempel med två oberoende källor.
V1 är spänningen orsakad av den oberoende strömkällan, V2 spänningen orsakad av den oberoende spänningskällan, V3 spänningen då båda är påslagna samtidigt. Notera hur nollade strömkällor/spänningskällor modeleras med avbrott/kortslutning respektive. Som superpositionsprincipen förutsa så är V3 = V2 + V1. Viktigt att komma ihåg är som sagt att resultatet bara gäller för kretsar bestående av Linjära komponenter. Den stora vinsten med superpositionsprincipen inser man kanske först man arbetar med Småsignalscheman.